CS61A(4): Higher-Order Functions

Posted on | In |

This is the lecture note of CS61A - Lecture 4.

Iteration Example

There are 2 different definitions of fib which can be used to calculate Fibonacci number.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def fib(n):
    """Compute the nth Fibonacci number, for N >= 1."""
    pred, curr = 0, 1   # 0th and 1st Fibonacci numbers
    k = 1               # curr is the kth Fibonacci number
    while k < n:
        pred, curr = curr, pred + curr
        k = k + 1
    return curr


def fib2(n):
    """Compute the nth Fibonacci number"""
    pred, curr = 1, 0
    k = 0
    while k < n:
        pred, curr = curr, pred + curr
        k = k + 1
    return curr

The second one is much better since it can computer the 0-th Fibonacci number correctly.

Designing Functions

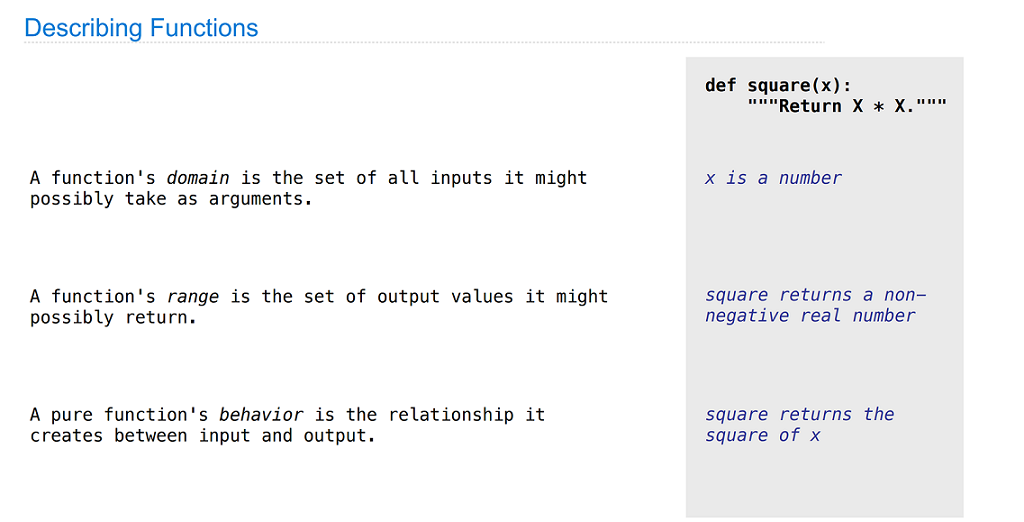
There are lots of different functions that can do the same thing, but some are better than others.

So, how to design better function?

🏜️ A Guide to Designing Function:

  • Give each function exactly one job.
  • Don’t repeat yourself (DRY). Implement a process just once, but execute it many times.
  • Define functions generally.

Example

The following is an example of generalizing patterns with arguments.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Compute the area of square, circle and hexoagon

from math import pi, sqrt

def area_square(r):
    """Return the area of a square with side length R."""
    return r * r

def area_circle(r):
    """Return the area of a circle with radius R."""
    return r * r * pi

def area_hexagon(r):
    """Return the area of a regular hexagon with side length R."""
    return r * r * 3 * sqrt(3) / 2

Noticing there are lots of repeating things among them.

Let's try to do some generalization.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Generalization: Generalizing patterns using arguments

def area(r, shape_constant):
    """Return the area of a shape from length measurement R."""
    assert r > 0, 'A length must be positive'
    return r * r * shape_constant

def area_square(r):
    return area(r, 1)

def area_circle(r):
    return area(r, pi)

def area_hexagon(r):
    return area(r, 3 * sqrt(3) / 2)

Higher-Order Function

The common structure among functions may be a computational process, rather than just a number we saw in the previous example.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Without generalization

def sum_naturals(n):
    """Sum the first N natural numbers.

    >>> sum_naturals(5)
    15
    """
    total, k = 0, 1
    while k <= n:
        total, k = total + k, k + 1
    return total

def sum_cubes(n):
    """Sum the first N cubes of natural numbers.

    >>> sum_cubes(5)
    225
    """
    total, k = 0, 1
    while k <= n:
        total, k = total + pow(k, 3), k + 1
    return total

We notice the above computational processes are similar. The only difference is how we deal with the value of k-th term.

Let's do generalization again.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Functions as arguments

from operator import mul

def identity(k):
    return k

def cube(k):
    return pow(k, 3)

def pi_term(k):
    return 8 / mul(k * 4 - 3, k * 4 - 1)

def summation(n, term):
    """Sum the first N terms of a sequence.

    >>> summation(5, cube)
    225
    """
    total, k = 0, 1
    while k <= n:
        total, k = total + term(k), k + 1
    return total

def sum_naturals(n):
    return summation(n, identity)

def sum_cubes(n):
    return summation(n, cube)

The function summation(n, term) above is called higher-order function, since it takes another function term as an argument.

Higher-order functions can also treat functions as return values. For example:

1
2
3
4
5
6
7
8
9
10
11
12
def make_adder(n):
    """Return a function that takes one argument K and returns K + N.

    >>> add_three = make_adder(3)
    >>> add_three(4)
    7
    """
    def adder(k):
        return k + n
    return adder

make_adder(2000)(20)

Higher-order functions :

  • express general methods of computation;
  • remove repetition from programs;
  • separate concerns among functions (each function just do one job)

Lambda Expression

Lambda expression is an expression that evalutes to a function.

1
2
3
4
5
6
7
# Lambda expressions

x = 10
square = x * x

square = lambda x: x * x
square(4)  # 16

Return Statements

A return statement completes the evaluation of a call expression and provides its value.

Let's look at 2 problems.

Question 1: find the smallest non-negative integer x which makes square(x) - 100 is positive

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def search(f):
    """Return the smallest non-negative integer x for which f(x) is a true value."""
    x = 0
    while True:
        if f(x):
            return x
        x += 1

def is_three(x):
    """Return whether x is three.

    >>> search(is_three)
    3
    """
    return x == 3

def square(x):
    return x * x

def positive(x):
    """A function that is 0 until square(x)-100 is positive.

    >>> search(positive)
    11
    """
    return max(0, square(x) - 100)

Question 2: define inverse function

1
2
3
4
5
6
7
8
9
def inverse(f):
    """Return a function g(y) that returns x such that f(x) == y
    * g(f(x)) -> x

    >>> sqrt = inverse(square)
    >>> sqrt(16)
    4
    """
    return lambda y: search(lambda x: f(x) == y)