CS61A(8): Recursion

Posted on | In |

This is the lecture note of CS61A - Lecture 8.

Recursive Function

A function is called recursive if the body of that function calls itself, either directly or indirectly.

Let's see an example.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Sum digits

def split(n):
    """Split a positive integer into all but its last digit and its last digit."""
    return n // 10, n % 10

def sum_digits(n):
    """Return the sum of the digits of positive integer n.

    >>> sum_digits(9)
    9
    >>> sum_digits(18117)
    18
    >>> sum_digits(9437184)
    36
    >>> sum_digits(11408855402054064613470328848384)
    126
    """
    # base cases
    if n < 10:
        return n
    # recursive case
    else:
        all_but_last, last = split(n)
        return sum_digits(all_but_last) + last

Another example:

1
2
3
4
5
6
7
8
9
10
11
12
# String reversal

def reverse_string(s):
    """Reverse a string s.

    >>> reverse_string('draw')
    'ward'
    """
    if len(s) == 1:
        return s
    else:
        return reverse_string(s[1:]) + s[0]

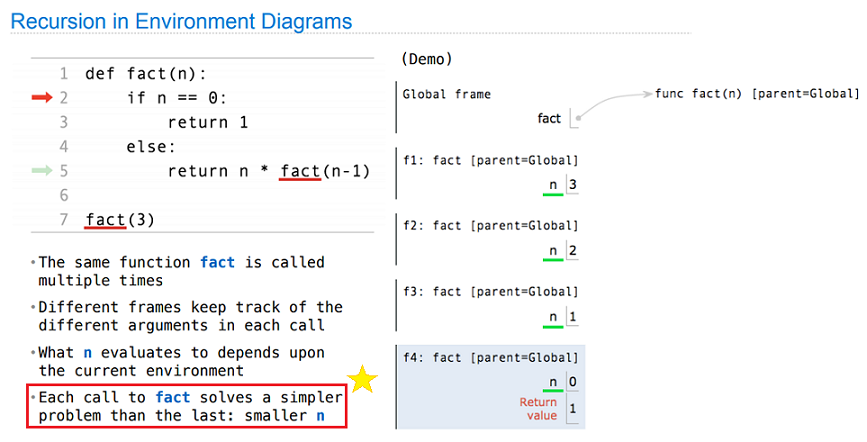
Recursion in Environment Diagrams

Notice: The recursion environment diagram is shown here to help you understand the recursive function execution process. When dealing with the real problems, you should avoid draw this environment diagrams.

Recursion and Iteration

Iteration is a special case of recursion. For the most of functions, you can convert from iteration into recursion, or vice versa.

Let's see another example.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Converting iteration to recursion

def sum_digits_iter(n):
    """Sum digits iteratively.

    >>> sum_digits_iter(11408855402054064613470328848384)
    126
    """
    digit_sum = 0
    while n > 0:
        n, last = split(n)
        digit_sum = digit_sum + last
    return digit_sum

def sum_digits_rec(n, digit_sum):
    """Sum digits using recursion, based on iterative version.

    >>> sum_digits_rec(11408855402054064613470328848384, 0)
    126
    """
    if n == 0:
        return digit_sum
    else:
        n, last = split(n)
        return sum_digits_rec(n, digit_sum + last)

Mutual Recursion

Mutual recursion occurs when two different functions call each other.

Let's see an example.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
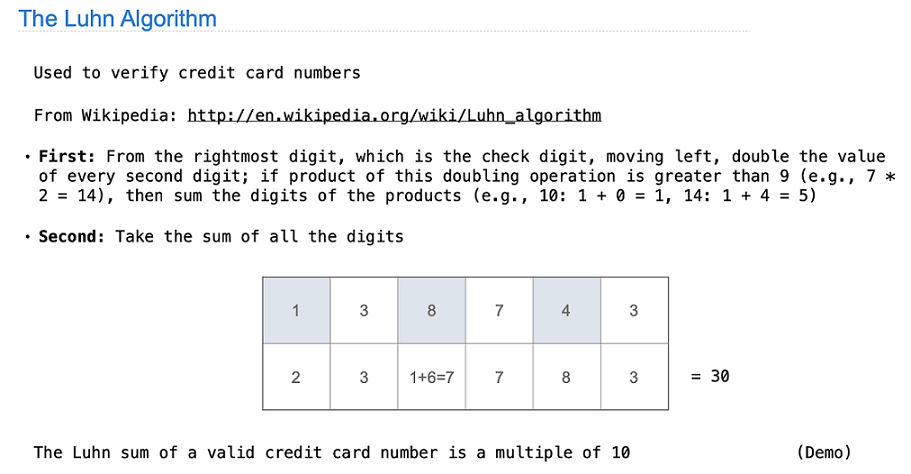
46
# Luhn algorithm: mutual recursion

def split(n):
    """Split a positive integer into all but its last digit and its last digit."""
    return n // 10, n % 10

def sum_digits(n):
    """Return the sum of the digits of positive integer n."""
    if n < 10:
        return n
    else:
        all_but_last, last = split(n)
        return sum_digits(all_but_last) + last

def luhn_sum(n):
    """Return the digit sum of n computed by the Luhn algorithm.

    >>> luhn_sum(2)
    2
    >>> luhn_sum(12)
    4
    >>> luhn_sum(42)
    10
    >>> luhn_sum(138743)
    30
    >>> luhn_sum(5105105105105100) # example Mastercard
    20
    >>> luhn_sum(4012888888881881) # example Visa
    90
    >>> luhn_sum(79927398713) # from Wikipedia
    70
    """
    if n < 10:
        return n
    else:
        all_but_last, last = split(n)
        return luhn_sum_double(all_but_last) + last

def luhn_sum_double(n):
    """Return the Luhn sum of n, doubling the last digit."""
    all_but_last, last = split(n)
    luhn_digit = sum_digits(2 * last)
    if n < 10:
        return luhn_digit
    else:
        return luhn_sum(all_but_last) + luhn_digit