CS61A(9): Tree Recursion

Posted on | In |

This is the lecture note of CS61A - Lecture 7.

Order of Recursive Calls

When making a function called, you have to wait for return before doing anything else.

Let's see an example.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Ordering

def cascade(n):
    """Print a cascade of prefixes of n.

    >>> cascade(1234)
    1234
    123
    12
    1
    12
    123
    1234
    """
    if n < 10:
        print(n)
    else:
        print(n)
        cascade(n//10)
        print(n)

# version 2
def cascade2(n):
    """Print a cascade of prefixes of n."""
    print(n)
    if n >= 10:
        cascade2(n//10)
        print(n)
  • If two implementations are equally clear, then shorter is usually better.
  • In this case, the longer implementation is more clear (at least to me).
  • When learning to write recursive functions, put the base cases first.
  • Both are recursive functions, even though only the first one has typical structure

Exercise : Write a function that prints an inverse cascade.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Inverse Cascade

def inverse_cascade(n):
    """Print an inverse cascade of prefixes of n.
    
    >>> inverse_cascade(1234)
    1
    12
    123
    1234
    123
    12
    1
    """
    grow(n)
    print(n)
    shrink(n)

def f_then_g(f, g, n):
    if n:
        f(n)
        g(n)

grow = lambda n: f_then_g(grow, print, n//10)
shrink = lambda n: f_then_g(print, shrink, n//10)

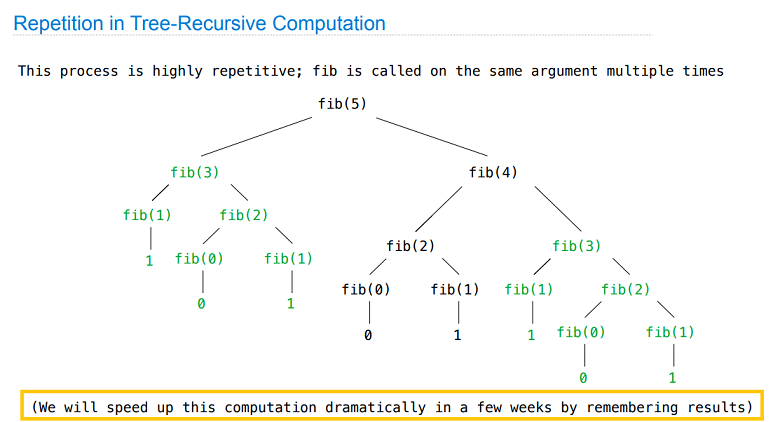
Tree Recursion

Tree-shaped processes arise whenever executing the body of a recursive function makes more than one recursive call.

Let's see an example :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Tree recursion

def fib(n):
    """Compute the n-th Fibonacci number.

    >>> fib(8)
    21
    """
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n-2) + fib(n-1)

Hanoi Tower

The Hanoi Tower Problem is a very classical recursion problem.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# Hanoi Tower

def print_move(origin, destination):
    """Print instructions to move a disk."""
    print("Move the top disk from rod", origin, "to rod", destination)

def move_stack(n, start, end):
    """Print the moves required to move n disks on the start pole to the end
    pole without violating the rules of Towers of Hanoi.

    n -- number of disks
    start -- a pole position, either 1, 2, or 3
    end -- a pole position, either 1, 2, or 3

    There are exactly three poles, and start and end must be different. Assume
    that the start pole has at least n disks of increasing size, and the end
    pole is either empty or has a top disk larger than the top n start disks.

    >>> move_stack(1, 1, 3)
    Move the top disk from rod 1 to rod 3
    >>> move_stack(2, 1, 3)
    Move the top disk from rod 1 to rod 2
    Move the top disk from rod 1 to rod 3
    Move the top disk from rod 2 to rod 3
    >>> move_stack(3, 1, 3)
    Move the top disk from rod 1 to rod 3
    Move the top disk from rod 1 to rod 2
    Move the top disk from rod 3 to rod 2
    Move the top disk from rod 1 to rod 3
    Move the top disk from rod 2 to rod 1
    Move the top disk from rod 2 to rod 3
    Move the top disk from rod 1 to rod 3
    """
    assert 1 <= start <= 3 and 1 <= end <= 3 and start != end, "Bad start/end"
    if n == 1:
        print_move(start, end)
    else:
        spare_peg = 6 - start - end         # find the spare pole
        move_stack(n-1, start, spare_peg)   # move the top (n - 1) disks from start to spare together (move these disks as a whole ... ABSTRACTION!)
        print_move(start, end)              # move the lowermost disk from start to end
        move_stack(n-1, spare_peg, end)     # move the (n - 1) disks from spare to end

"""
time complexity: O(2^n) ... more details in CS61B & CS170!
"""

Example: Counting Partitions

Let's see an important example of tree recursion —— counting partitions of an integer.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def count_partitions(n, m):
    """Count the partitions of n using parts up to size m.

    >>> count_partitions(6, 4)
    9
    >>> count_partitions(10, 10)
    42
    """
    # base case
    if n == 0:
        return 1
    elif n < 0:
        return 0
    elif m == 0:
        return 0
    #recursive case
    else:
        with_m = count_partitions(n-m, m)
        without_m = count_partitions(n, m-1)
        return with_m + without_m